Python, GAs, TSP and a lot of Optimization

Together with some friends we built a python library for Genetic Algorithms (GAs), specifically aimed at constraint optimization problems. The core focus was on building a well-performing GA for solving the Travelling Salesman Problem (TSP). TSP is a commonly studied NP-hard problem in computational optimization; essentially, given a list of cities we need to determine the best possible route - the shortest possible route.
The code can be found at: https://github.com/daveai/GA_Library
The team: daveai - ruifcruz - GustavoFabricio - statoconfusionale
We built our GAs on top of the core framework provided by Fernando Perez
Firstly, we set down the decision variables for the TSP GA. Classic TSP determines that cities should be visited only once and that the salesman return to their original destination at the end of the trip. To encode this we simply used a permutation of the length of total cities. We include the “home-trip” in the fitness function (the function which calculates the distance, which in our case represents the fitness of the solution). Given that we want to minimize the distance, it’s important to note that all the methods we implemented work with both minimization and maximization constraint optimization problems.
For the city data we implemented our GA to work both with a matrix of coordinates, as well as simply supplying the coordinates of the cities - from which we then build a matrix of coordinates. From our research in the literature, TSP doesn’t typically specify a starting city, which means there are at least as many global solutions as there are cities - as the global optima permutation would have the same fitness starting at any city within that permutation.
from scipy.spatial.distance import squareform, pdist
import numpy
def coordsToDist(coords):
"""
Util function to transform a table of coords into a matrix of distances
param coords: list of N rows and 2 columns (x and y)
return matrix of NxN distances
"""
coordinates_array = numpy.array(coords)
dist_array = pdist(coordinates_array)
return squareform(dist_array)
To initialize a “tour” we implemented two methods: a purely stochastic one, where we simply create a random permutation, as well as a deterministic one, which creates a tour by selecting a random city and then always appending its nearest available neighbour. The only constraint of TSP is that a tour be a permutation.
def build_solution(self):
"""Builds a linear solution for TSP with a specific order of cities"""
solution_representation = []
encoding_data = self._encoding.encoding_data
# Choose an initial random city
solution_representation.append(randint(1, len(encoding_data)))
# Build a solution by appending the closest available city
for i in range(len(encoding_data)):
dists = [x for x in self._distances[solution_representation[-1] - 1]]
sorDist = sorted(dists)
for j in sorDist:
if (dists.index(j) + 1) not in solution_representation:
solution_representation.append(dists.index(j) + 1)
break
solution = LinearSolution(
representation=solution_representation, encoding_rule=self._encoding_rule
)
return solution
When thinking about the TSP GA we wanted to achieve good fitness, but also find solutions quickly. Therefore, we constantly profiled our code and managed to reduce execution time by roughly 85% by keeping computational intensity in mind, with some minor memory enhancements. Initially all new offsprings were deepcopied - and since individuals were classes, deepcopy recursively iterated over every individual. We instead implemented a simple_copy function within the class, which is much quicker yet preserves all the metadata of the offspring.
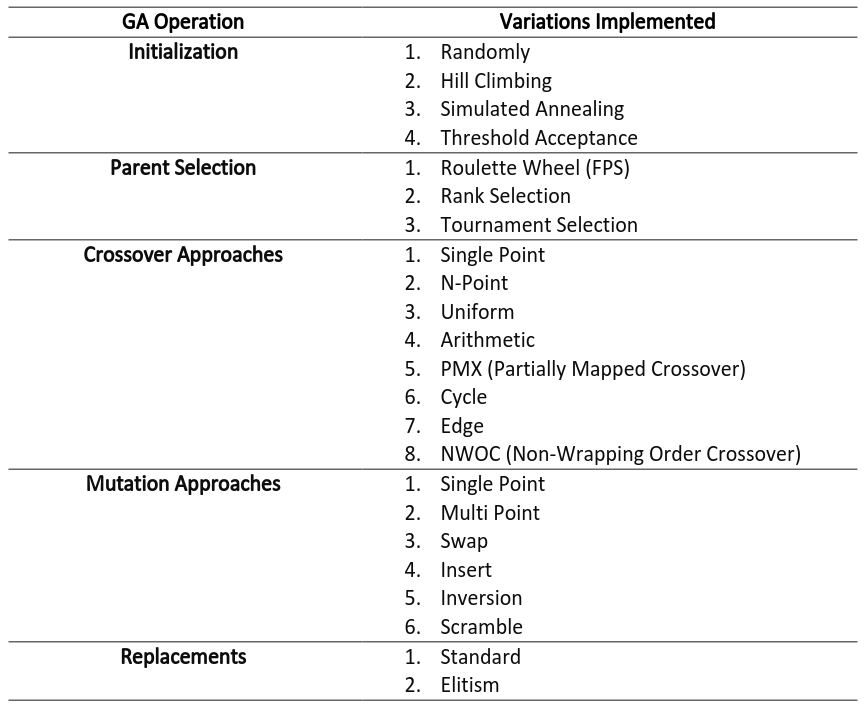
We implemented all of the operators below (these were implemented agnostically from TSP, and can be simply used with any GA problem):
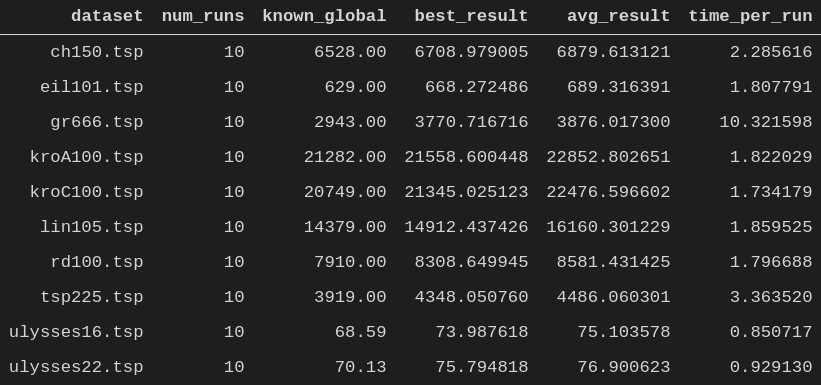
Below are some benchmarks, based on popular TSP datasets retrieved from Universität Heidelberg. Discrete and Combinatorial Optimization. Available at: http://comopt.ifi.uni-heidelberg.de/software/TSPLIB95/tsp/ As we can see the GA comes close to global optima in most datasets, and it does so within seconds.
We also coded a GA Optimizer GA (a GA to optimize the parameters of our TSP GA), which ran over a number of hours to fine tune the parameters of our TSP GA, the optimal parameters we found are these:
Parameters: {
"Population-Size": 20,
"Number-of-Generations": 1000,
"Crossover-Probability": 0.1,
"Mutation-Probability": 0.8,
"Initialization-Approach": initialize_using_hc,
"Selection-Approach": TournamentSelection,
"Tournament-Size": 20,
"Crossover-Approach": pmx_crossover,
Mutation-Aproach": inversion_mutation,
"Replacement-Approach": elitism_replacement}
It intuitively makes sense that crossover has a low probability given that a tour makes gradual improvements through mutations, and crossovers move more cities around. Imagine for instance we’re at the final generations and have a decent fitness, it’s more likely we can “close an edge” through mutation and increase fitness than by using crossover which will alter the position of many cities. This holds true even with specific crossover techniques aimed specifically at TSP.
For further reading on TSP and GAs I can recommend:
Dueck, G. and Scheuer, T. (1990). Threshold accepting: A general purpose optimization algorithm appearing superior to simulated annealing. Journal of Computational Physics, 90(1), pp.161-175.
Eiben, A. and Smith, J. (2015). Introduction to Evolutionary Computing, Second Edition. 2nd ed. Berlin Heidelberg: Springer.
Larrañaga, P., Kuijpers, C., Murga, R., Inza, I. and Dizdarevic, S. (1999). Artificial Intelligence Review, 13(2), pp.129-170.
Lin, S. and Kernighan, B. (1973). An Effective Heuristic Algorithm for the Traveling-Salesman Problem. Operations Research, 21(2), pp.498-516.